En la teoría de grafos, el problema de los caminos más cortos es el problema que consiste en encontrar un camino entre dos vértices (o nodos) de tal manera que la suma de los pesos de las aristas que lo constituyen es mínima. Un ejemplo es encontrar el camino más rápido para ir de una ciudad a otra en un mapa. En este caso, los vértices representan las ciudades, y las aristas las carreteras que las unen, cuya ponderación viene dada por el tiempo que se emplea en atravesarlas.
Los algoritmos más importantes para resolver este
problema son:
·
Algoritmo de Dijkstra, resuelve el problema de los caminos más
cortos desde un único vértice origen hasta todos los otros vértices del grafo.
·
Algoritmo de Bellman - Ford, resuelve el problema de los caminos más cortos
desde un origen si la ponderación de las aristas es negativa.
·
Algoritmo de Búsqueda A*, resuelve el problema de los caminos más
cortos entre un par de vértices usando la heurística para intentar agilizar la búsqueda.
·
Algoritmo de Floyd - Warshall, resuelve el problema de los caminos más cortos
entre todos los vértices.
·
Algoritmo de Johnson, resuelve el problema de los caminos más cortos
entre todos los vértices y puede ser más rápido que el de Floyd - Warshall en
grafos de baja densidad.
·
Teoría perturbacional, encuentra en el peor de los casos el camino más
corto a nivel local.
ALGORITMO DE DIJKSTRA
Presentaremos un
algoritmo descubierto por el físico holandés Edsger Dijkstra en 1959. La
versión que descubriremos resuelve este problema para grafos ponderados no
dirigidos si todos los pesos no son negativos. Este algoritmo puede adaptarse
fácilmente para resolver problemas de caminos de longitud mínima en grafo
dirigidos.
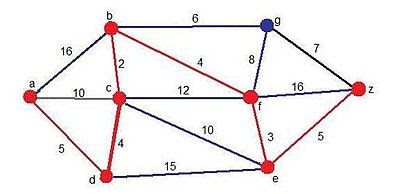
El siguiente ejemplo se desarrollará con el fin
de encontrar el camino más corto desde a hasta z- Rojo:
Aristas y vértices pertenecientes a la solución momentánea.
- Azul:
Aristas y vértices candidatos.
Paso 1
En e
- Distancia:5
Paso 2
Ahora, vemos que se añade un nuevo candidato, el
vértice e, y el vértice c, pero esta vez a través del d. Pero el camino mínimo
surge al añadir el vértice c.
Solución momentánea:
- Camino:
ADC
- Distancia:9
Paso 3
En este paso se añade como candidato el vértice f.
En este caso el camino mínimo hallado es el siguiente:
Solución momentánea:
- Camino:
ADCB
- Distancia:11
Paso 4
Como podemos comprobar, se han añadido un candidato
nuevo, el vértice g, a través del vértice b. El mínimo camino hallado en todo
el grafo hasta ahora es el siguiente:
Solución momentánea:
- Camino:
ADCBF
- Distancia:15
Paso 5
En este antepenúltimo paso, se añaden tres vértices
candidatos, los vértices g, z y e. Este último ya estaba pero en esta ocasión
aparece a través del vértice f. En este caso el camino mínimo, que cambia un
poco con respecto al enterior, es:
Solución momentánea:
- Camino:
ADCBG
- Distancia:17
Paso 6
En el penúltimo paso, vuelve a aparecer otro
candidato: el vértice e, pero esta vez a través del vértice f. De todas formas,
el camino mínimo vuelve a cambiar para retomar el camino que venía siguiendo en
los pasos anteriores:
Solución momentánea:
- Camino:
ADCBFE
- Distancia:18
Paso 7
Por fin, llegamos al último paso, en el que sólo se
añade un candidato, el vértice z a través del e. El camino mínimo y final
obtenido es nada mas y nada menos k:
Solución Final:
- Camino:
ADCBFEZ
- Distancia:23